Question

Give the equation of the line parallel to a line through (-3, 4) and (-5, -6) that passes through the origin. y = 5x y = 5x + 1 y=-1/5x + 1 y = -1/5x y

Answer 1

To solve for the equation of the line parallel :

`\begin{gathered} (-3,4)\Longrightarrow(x_1,y_1) \\ (-5,-6)\Longrightarrow(x_2,\text{y}_2) \end{gathered}`

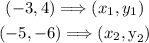
For parallel line equation:

Slope-intercept form: y=mx+b, where m is the slope and b is the y-intercept

First let's find the slope of the line.

To find the slope using two points, divide the difference of the y-coordinates by the difference of the x-coordinates.

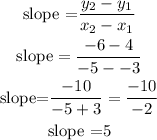
`\begin{gathered} \text{slope =}(y_2-y_1)/(x_2-x_1) \\ \text{slope}=(-6-4)/(-5--3) \\ \text{slope=}(-10)/(-5+3)=(-10)/(-2) \\ \text{slope =5} \end{gathered}`

Slope= 5

`\begin{gathered} y=mx+c \\ y=5x+c \\ \text{where c = y-intercept} \end{gathered}`

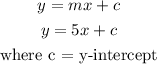
The y-intercept is (0, b). The equation passes through the origin, so the y-intercept is 0.

`\begin{gathered} y=5x+0 \\ y=5x \end{gathered}`

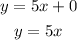
Hence the