Question

I need help I already answered just to make sure

Answer 1

The height of the tree is 13.82 m

Step - by - Step Explanation

What to find? Height of the tree.

Given:

• Angle of elevation = 62,°

,

• Eye-level above the ground =160cm

,

• Distance away from the tree = 6.5m

We need to first sketch the problem, to have a clearer picture of the question.

Change 160cm to meter

160 cm = 160/100 = 1.6 m

Height of the tree = 1.6 + x

We need to find the value of x.

From the sketch above;

Opposite =x

Adjacent =6.5

θ= 62°

Using the trigonometric ratio;

`\tan \theta=\frac{opposite\text{ }}{\text{adjacent}}`

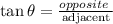
Substitute the values.

`\tan 62=(x)/(6.5)`

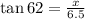
Cross-multiply.

x=6.5tan62°

x = 12.22 m

Height of the tree = 1.6 m + 12.22m

Height of the tree = 13.82 m

OR

Height of the tree = 1382 cm approximately.