Question

Por C?AnswerExample0 How many ways can 4 candy bars be chosenfrom a store that sells 30 candy bars?С27,4052 How many ways can 13 students line up for lunch?113 How many ways can you make a 3-letterarrangements out of the letters in the wordTRAPEZOID.4 How many ways can you choose 2 books from ashelf of 40 books-5 How many ways can 12 swimmers finish in first,second, and third place?.L11---How many ways can Mrs. Sullivan choose twostudents from 27 to help put away calculators atthe end of class?----1-111

Answer 1

1) How many ways can 4 candy bars be chosen from a store that sells 30 candy bars?

In this case we can combine 30 types of candy bars in a set of 4 bars.

This can be calculated as a combination of 30 in 4 with no repetition:

`\begin{gathered} C(n,r)=(n!)/((n-r)!r!) \\ C(30,4)=(30!)/((30-4)!4!)=(30!)/(26!4!)=(30\cdot29\cdot28\cdot27)/(4\cdot3\cdot2\cdot1)=(657720)/(24)=27405 \end{gathered}`

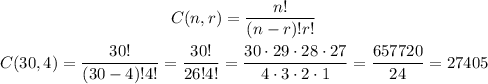
Answer: 27,405 possible combinations (C).

2) How many ways can 13 students line up for lunch?

In this case we have a permutation of 13 in 13 with no repetition.

We can calculate this as:

`\begin{gathered} P(n,r)=(n!)/((n-r)!) \\ P(13,13)=(13!)/((13-13)!)=(13!)/(1)=6227020800 \end{gathered}`

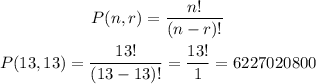
Answer: 6,227,020,85)00 possible permutations (P).

3) How many ways can you make a 3-letter arrangements out of the letters in the word TRAPEZOID.

In the word we have 9 letters with no repetition, so we have to calculate a permutation (as order matters) of 9 letters in 3 places.

We can calculate this as:

`P(9,3)=(9!)/((9-3)!)=(9!)/(6!)=9\cdot8\cdot7=504`

Answer: 504 possible permutations (P).

4) How many ways can you choose 2 books from a shelf of 40 books.

In this case, the order does not matter, so it is a combination of 40 in 2.

This can be calculated as:

`C(40,2)=(40!)/((40-2)!2!)=(40!)/(38!2!)=(40\cdot39)/(2\cdot1)=(1560)/(2)=780`

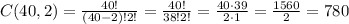
Answer: 780 possible combinations (C)

5) How many ways can 12 swimmers finish in first, second, and third place?

In this case, the order does matter, so we have a permutation of 12 in 3:

`P(12,3)=(12!)/((12-3)!)=(12!)/(9!)=12\cdot11\cdot10=1320`

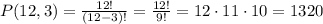
Answer: 1320 permutations (P)

6) How many ways can Mrs. Sullivan choose two students from 27 to help put away calculators at the end of class?

The order does not matter between the two students, so it is a combination of 27 in 2:

`C(40,2)=(27!)/(25!2!)=(27\cdot26)/(2\cdot1)=351`

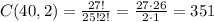
Answer: 351 combinations (C)