Part A.
Given:
P = (5, 4), Q = (7, 3), R = (8, 6), S = (4, 1)
Let's find the component of the vector PQ + 5RS.
To find the component of the vector, we have:
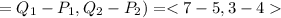
For vector RS, we have:
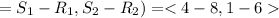
Hence, to find the vector PQ+5RS, we have:
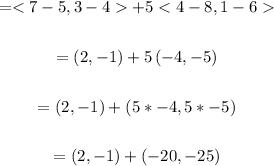
Solving further:
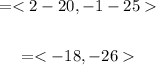
Therefoee, the component of the vector PQ+5RS is:
<-18, -26>
• Part B.
Let's find the magnitude of the vector PQ+5RS.
To find the magnitude, apply the formula:
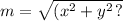
Thus, we have:
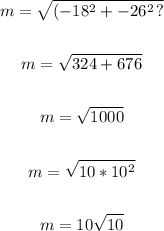
Therefore, the magnitude of the vector is:
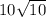
ANSWER:
Part A. <-18, -26>
Part B. 10√10