To solve this problem, we will first find the standard form of the circle equation. Given a circle of radius r and center (h,k), the standard form of the circle equation would be

In our case, we have h=8 , k=6 and r=10. So the equation for the given circle would be
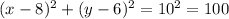
The general form of the circle equation can be obtained from expanding the squares on the left side of the equality sign. Recall that
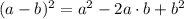
So, applying this to the standard equation we get


So our equation becomes
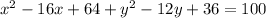
Operating on the left side, we have
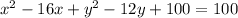
By subtracting 100 on both sides, we get
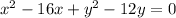
which the general form of the equation of the given circle.
Using a graphing tool, we have that the circle's graph would be