Question

question 18:Evaluate: summation from n equals 2 to 8 of 12 times 4 tenths to the n plus 1 power period Round to the nearest hundredth. (1 point)

Answer 1

Given:

`\sum_{n\mathop{=}2}^812(0.4)^(n+1)`

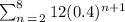
Required:

Sum of the numbers

Step-by-step explanation:

Let

`A_n=\sum_{n\mathop{=}2}^812(0.4)^(n+1)`

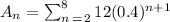
when n = 2, Aₙ becomes

`A_2=12(0.4)^(2+1)=12*(0.4)^3=0.768`

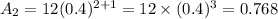
when n = 3, Aₙ becomes

`A_3=12(0.4)^(3+1)=12*(0.4)^4=0.3072`

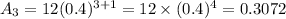
when n = 4, Aₙ becomes

`A_4=12(0.4)^(4+1)=12*0.4^5=0.12288`

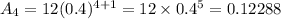
when n = 5, Aₙ becomes

`A_5=12(0.4)^(5+1)=12*0.4^6=0.049152`

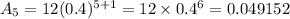
when n = 6, Aₙ becomes

`A_6=12(0.4)^(6+1)=12*0.4^7=0.0196608`

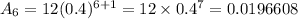
when n = 7, Aₙ becomes

`A_7=12(0.4)^(7+1)=12*0.4^8=0.007866432`

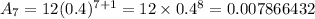
when n = 8, Aₙ becomes

`A_8=12(0.4)^(8+1)=12*0.4^9=0.003145728`

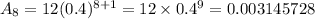
So now,

`\begin{gathered} A=A_1+A_2+A_3+A_4+A_5+A_6+A_7+A_8 \\ \\ A=0.768+0.3072+0.12288+0.049152+0.0196608+0.00786432+0.003145728 \\ \\ A=1.277902848\approx1.28 \end{gathered}`

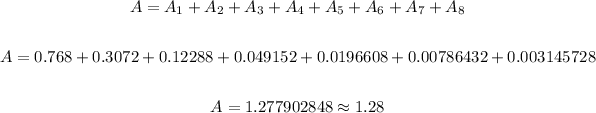
Final answer:

The