To calculate the interest earned, we can use the following equation:

Where P is the value of the deposit, i is the interest rate and n is the number of periods of time.
First, we need to calculate the equivalent value of 1 1/8 % as:

So, replacing P by $50,000, i by 0.01125, and n by 6, we get:
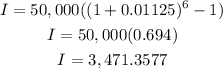
Answer: $ 3,471.3577