Question

This is not from a test or graded assessment. The Question is included in the picture.

Answer 1

Given:

`\begin{gathered} g(x)=-x^5-4x^3+6x \\ \\ h(x)=x^4+2x^3-2x^2+x-7 \\ \\ j(x)=3x^4+7x^2 \end{gathered}`

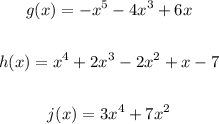
It's required to determine if the functions are odd, even, or neither.

An even function satisfies the property:

f(-x) = f(x).

And an odd function satisfies the property:

f(-x) = -f(x)

We substitute x by -x on each function as follows:

`\begin{gathered} g(-x)=-(-x)^5-4(-x)^3+6(-x) \\ \\ g(-x)=x^5+4x-6x \end{gathered}`

Note the function g(-x) is the inverse (negative) of g(x), thus,

g(x) is odd

Now test h(x):

`\begin{gathered} h(-x)=(-x)^4+2(-x)^3-2(-x)^2+(-x)-7 \\ \\ h(-x)=x^4-2x^3-2x^2-x-7 \end{gathered}`

Comparing h(-x) and h(x) we can see none of the properties are satisfied, thus:

h(x) is neither odd nor even

Let's now test j(x):

`\begin{gathered} j(-x)=3(-x)^4+7(-x)^2 \\ \\ j(-x)=3x^4+7x^2 \end{gathered}`

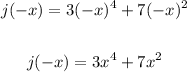
Since j(-x) and j(x) are equal,

j(x) is even