Question

Please help with statistic 7

Answer 1

Part 1

Answer: Choice C only

No, the random variable x is categorical instead of numerical

Step-by-step explanation:

The term "categorical" is the same as "nominal". Either refers to data labels or names, rather than numbers. The three categories are: Left, Right, No preference. We cannot apply math operations to names like this. It makes no sense to average Left vs Right vs No Preference.

==========================================================

Part 2

Answer: B) The table does not show a probability distribution

Step-by-step explanation:

Recall that the value of mu is calculated like so:
`\mu = \sum xp(x)`

In other words, we multiply each x value with its corresponding p(x) probability. Then we add up those results to get mu. There's one glaring problem though: we aren't given numeric values for x. So there's no way to compute any of the x*p(x) values. Therefore, we don't have a mu value either. It doesn't make sense to determine what the center is when given labels. We would need x to take on values from the set {0,1,2,3,...} if we wanted to compute a mu value.

==========================================================

Part 3

Answer: B) The table does not show a probability distribution

Explanation:

The value of sigma depends heavily on the value of mu.

One formula for sigma is
`\displaystyle \sigma = \sqrt{p(x_i)*\sum_(i=1)^(n)(x_i-\mu)^2`

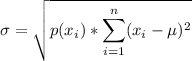
which is often abbreviated to
`\displaystyle \sigma = \sqrt{p(x)*\sum(x-\mu)^2`

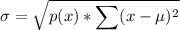
Because we can't find mu, we can't find sigma either.

Also, it makes no sense to determine how spread out categorical labels are. How can we determine the distance from "Left" to "Right"? The x values need to be numeric so we can calculate a numeric standard deviation from it.