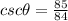Question

Suppose theta is an angle in the standard position whose terminal side is in quadrant 1 and sin theta = 84/85. find the exact values of the five remaining trigonometric functions of theta

Answer 1

we know that

The angle theta lies in the I quadrant

`sin\theta=(84)/(85)`

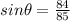
step 1

Find out the value of the cosine of angle theta

Remember that

`sin^2\theta+cos^2\theta=1`

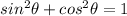
substitute given value

`\begin{gathered} ((84)/(85))^2+cos^2\theta=1 \\ \\ cos^2\theta=1-(7,056)/(7,225) \\ \\ cos^2\theta=(169)/(7,225) \\ \\ cos\theta=(13)/(85) \end{gathered}`

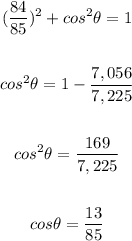
step 2

Find out the value of the tangent of angle theta

`tan\theta=(sin\theta)/(cos\theta)`

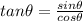
substitute given values

`\begin{gathered} tan\theta=((13)/(85))/((84)/(85))=(13)/(84) \\ therefore \\ tan\theta=(13)/(84) \end{gathered}`

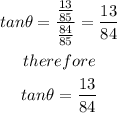
step 3

Find out the cotangent of angle theta

`cot\theta=(1)/(tan\theta)`

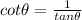
therefore

`cot\theta=(84)/(13)`

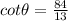
step 4

Find out the value of secant of angle theta

`sec\theta=(1)/(cos\theta)`

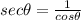
therefore

`sec\theta=(85)/(13)`

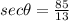
step 5

Find out the value of cosecant of angle theta

`csc\theta=(1)/(sin\theta)`

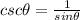
therefore

`csc\theta=(85)/(84)`