Question

A line passes through the points (2,5) and (-6,4). What is it's equation in point-slope form?

Answer 1

y-5=⅛(x-2)

Step-by-step explanation:

Given the points (2,5) and (-6,4).

To find the equation of the line joining these points in point-slope form, we begin by finding its slope.

`\begin{gathered} \text{Slope,m}=\frac{Change\text{ in y-axis}}{Change\text{ in x-axis}} \\ =(5-4)/(2-(-6)) \\ =(1)/(2+6) \\ m=(1)/(8) \end{gathered}`

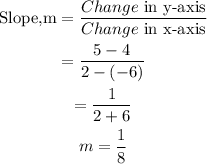
Next, we substitute the slope and any of the given points into the point-slope form below:

`y-y_1=m(x-x_1)`

We use the point (2,5).

• x1=2, y1=5

`y-5=(1)/(8)(x-2)`

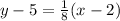
The equation in point-slope form is y-5=⅛(x-2).