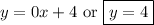Question

Find the equation of the line parallel to the line y=-1, going through point (-5,4)

Answer 1

In this problem, want to find the equation of a line that will be parallel to a given function through a point.

Recall that parallel lines have the same slope.

We are given the line

`y=-1`

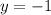
and the point

`(-5,4)`

Notice that the equations is technically in slope-intercept form, by the value of the slope will be 0:

`y=0x-1`

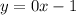
Therefore, the slope of the line through (-5,4) will also be zero. We can use that information to find the equation.

Using the form

`y=mx+b`

we can substitute the point and the slope to solve for b:

`\begin{gathered} 4=0(-5)+b \\ \\ 4=b \end{gathered}`

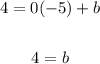
So, the equation of our line is:

`y=0x+4\text{ or }\boxed{y=4}`