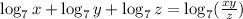Question

I have a practice problem that I need help on.These are included in the problem as well Where did Arjun make errors?Explain his errors and the properties of logarithms that leads to the answer. State the correct answer.

Answer 1

Arjun applied the wrong laws of logarithms.

The question can be solved as shown below:

`\log _7x+\log _7y+\log _7z`

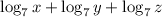
Step 1: Apply the addition rule of logarithm given as

`\log _am+\log _an=\log _a(m\cdot n)`

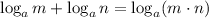
Thus, we have:

`(\log _7x+\log _7y)+\log _7z=\log _7(x\cdot y)+\log _7z`

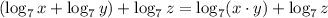
Step 2: Apply the subtraction rule of logarithm given as

`\log _am-\log _an=\log _a((m)/(n))`

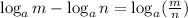
Thus, we have:

`\log _7(x\cdot y)+\log _7z=\log _7((x\cdot y)/(z))`

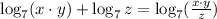
Therefore, the correct answer is:

`\log _7x+\log _7y+\log _7z=\log _7((xy)/(z))`