Question

A car is negotiating a flat circular curve of radius 50 m with a speed of 20 m/swithout slipping. The maximum centripetal force (provided by static friction) is 1.2 x10^4N. What is the mass of the car?1) 0.50 x 10^3 kg2) 1.0 x 10^3 kg3) 1.5 x 10^3kg4) 2.0 x 10^3 kg

Answer 1

We are given a car that is experiencing a centripetal force.

The formula for the force is given by:

`F_c=(mv^2)/(r)`

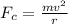
Where "m" is the mass, "v" is the velocity and "r" is the radius. Now we solve for the mass, first by multiplying both sides by r:

`rF_c=mv^2`

Now we divide by the velocity squared:

`(rF_c)/(v^2)=m`

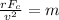
Now we replace the known values:

`((50m)(1.2*10^4N))/((20(m)/(s))^2)=m`

Solving the operations:

`1500kg=m`

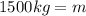
Therefore, the mass is 1500 kg.