To find the solution we need to graph both lines on the plane. To do this we need to find two points for each line.
First we graph the line y=x+2. To find a point we give x a value, whichever value we like, and then find y.
Let x=0, then:

Then we have the point (0,2).
Let x=1, then:

Then we have the point (1,3).
Then we plot this points in the plane and join them with a line:
Now let's plot eh second line, y=3x-4.
Let x=0, then:
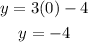
So we have the points (0,-4).
Let x=1, then:
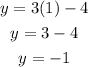
so we have the point (1,-1).
Now we plot this points and join them with a line:
Once we have both lines graph in the plane the solution is the intersection of the lines. Looking at the graph we conclude that the solution of the system is x=3 and y=5.