Question

End Behavior Graphically

Answer 1

We will investigate how to determine the end behaviours of polynomial functions.

The function given to us is:

`f(x)=123x^3+9x^4-786x-3x^{5^{}}-189x^2\text{ + 1260}`

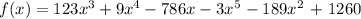
Whenever we try to determine the end-behaviour of any function. We are usually looking for value of f ( x ) for the following two cases:

`x\to\infty\text{ and x}\to-\infty`

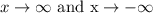
The most important thing to note when dealing with end-behaviour of polynomial functions is that the behaviour is pre-dominantly governed by the highest order term of a polynomial. The rest of the terms are considered small or negligible when considering end-behaviours of polynomials.

The highest order terms in the given function can be written as:

`f(x)=-3x^5`

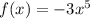
Then the next step is to consider each case for the value of ( x ) and evaluate the value of f ( x ) respectively.

`\begin{gathered} x\to\infty \\ f\text{ ( }\infty\text{ ) = -3}\cdot(\infty)^5 \\ f\text{ ( }\infty\text{ ) = -3}\cdot\infty \\ f\text{ ( }\infty\text{ ) = -}\infty \end{gathered}`

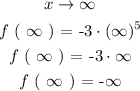
Similarly repeat the process for the second case:

`\begin{gathered} x\to-\infty \\ f\text{ ( -}\infty\text{ ) = -3}\cdot(-\infty)^5 \\ f\text{ ( -}\infty\text{ ) = 3}\cdot\infty \\ f\text{ ( -}\infty\text{ ) = }\infty \end{gathered}`

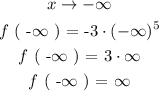
Combining the result of two cases we get the following solution:

`As\text{ x}\to\text{ }\infty\text{ , y}\to\text{ -}\infty\text{ and as x}\to-\infty\text{ , y}\to\text{ }\infty`

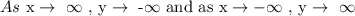
Correct option is:

`\text{Option C}`