Question

3: A Bunch of SystemsSolve each system of equations without graphing and show your reasoning. Then, check yoursolutions,

Answer 1

Use the elimination method to solve the given system of equations.

To do so, multiply the first equation by -3 so that the coefficient of x in the first equation becomes the additive inverse of the coefficient of x in the second equation:

`\begin{gathered} -3(2x+3y)=-3(16) \\ \Rightarrow-6x-9y=-48 \end{gathered}`

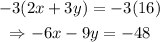
Then, the system is equivalent to:

`\begin{gathered} -6x-9y=-48 \\ 6x-5y=20 \end{gathered}`

Add both equations to eliminate the variable x and to obtain an equation in terms of the variable y only:

`\begin{gathered} (-6x-9y)+(6x-5y)=-48+20 \\ \Rightarrow-6x-9y+6x-5y=-28 \\ \Rightarrow-14y=-28 \\ \Rightarrow y=(-28)/(-14) \\ \therefore y=2 \end{gathered}`

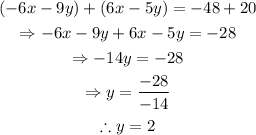
Replace y=2 into the first equation to find the value of x:

`\begin{gathered} 2x+3y=16 \\ \Rightarrow2x+3(2)=16 \\ \Rightarrow2x+6=16 \\ \Rightarrow2x=16-6 \\ \Rightarrow2x=10 \\ \Rightarrow x=(10)/(2) \\ \therefore x=5 \end{gathered}`

Replace y=2 and x=5 into the second equation to confirm the answer:

`\begin{gathered} 6x-5y=20 \\ \Rightarrow6(5)-5(2)=20 \\ \Rightarrow30-10=20 \\ \Rightarrow20=20 \end{gathered}`

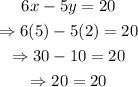
Therefore, the solution to the system of equations is x=5, y=2.