Question

The exponential function that represents an experiment to track the growth of agroup bacterial cells is f(x) = 2200(1.03)*, where f(x) is the number of cells and x isthe time in minutes.• Sketch this scenario, including variables, title, axes and appropriate scales.• How many bacterial cells were there to begin the experiment?• What is the percentage growth of the bacterial cells per minute?• How many bacterial cells are there after one-half hour? Round to the nearestthousand.• How long will it take for there to be 7500 bacterial cells? Round your answerto the nearest whole minute?

Answer 1

For this problem we are going to be working with the function:

`f(x)=2200(1.03)^x`

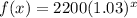
where x is the time in minutes and f(x) represents the number of bacteria at any given time x.

Part 1.

To sketch the graph we need to determine some points of it; to get them we give values to x and plug them in the expression for the funtion.

If x=0 we have that:

`\begin{gathered} f(0)=2200(1.03)^0 \\ f(0)=2200 \end{gathered}`

Then we have the point (0,2200).

If x=10 we have that:

`\begin{gathered} f(10)=2200(1.03)^(10) \\ f(10)=2956.616 \end{gathered}`

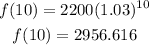
Then we have the point (10,2956.616).

If x=20 we have that:

`\begin{gathered} f(20)=2200(1.03)^(20) \\ f(20)=3973.445 \end{gathered}`

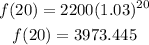
Then we have the point (20,3973.445).

If x=30 we have that:

`\begin{gathered} f(30)=2200(1.03)^(30) \\ f(30)=5339.977 \end{gathered}`

Then we have the point (30,5339.977).

If x=40 we have that:

`\begin{gathered} f(40)=2200(1.03)^(40) \\ f(40)=7176.483 \end{gathered}`

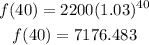
Then we have the point (40,7176.483).

If x=50 we have that:

`\begin{gathered} f(50)=2200(1.03)^(50) \\ f(50)=9644.593 \end{gathered}`

Then we have the point (50,9644.593).

Then we have the points (0,2200), (10,2956.616), (20,3973.445), (30,5339.977), (40,7176.483) and (50,9644.593). Plotting this points on the plane and joining them with a smooth line we have that the grah of the function is:

Part 2.

To determine how many bacteria were at the beginnning of the experiment we plug x=0 in the function describing the population, we did this in the previous question; therefore we conclude that there were 2200 bacteria at the beginning of the experiment.

Part 3.

We notice that the function fgiven has the form:

`f(x)=a(1+r)^x`

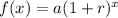
where a=2200 and r=0.03; for this type of function the growth rate in decimal form is given by r. Therefore we conclude that the percentage growth in this function is 3%.

Part 4.

To determine how many bacteria were in the experiment after one half hout we plug x=30 in the function give; we did this in part 1 of the proble.Therefore we conclude that after one half hour there were approximately 5340 bacteria cells. (for this part we roun to the neares whole number)

Part 5.

To determine how long it takes to have 7500 cells we plug f(x)=7500 in the expression given and solve the resulting equation for x:

`\begin{gathered} 2200(1.03)^x=7500 \\ 1.03^x=(7500)/(2200) \\ 1.03^x=(75)/(22) \end{gathered}`

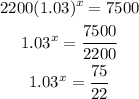
To remove the base we need to remember that:

`b^y=x\Leftrightarrow y=\log _bx`

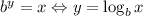
Then we have:

`\begin{gathered} 1.03^x=(75)/(22) \\ x=\log _(1.03)((75)/(22)) \end{gathered}`

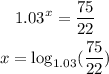
Now we use the change of base property for logarithms:

`\log _bx=(\ln x)/(\ln b)`

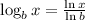
Then we have:

`\begin{gathered} x=\log _(1.03)((75)/(22)) \\ x=(\ln ((75)/(22)))/(\ln 1.03) \\ x=41.491 \end{gathered}`

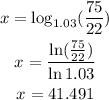
Therefore it takes 41 minutes to have 7500 cells.