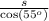Question

The picture shows a triangular island:Which expression shows the value of q?s over sin 55 degreess over cos 55 degreesr sin 55°r cos 55°q?

Answer 1

A right triangle is a triangle with a right angle. The opposite side to the right angle is called the hypotenuse and the other sides are the legs. Given an angle in a right triangle, the ratio between the leg adjacent to the angle and the hypotenuse is equal to the cosine of the angle.

Using this relation in our problem, we have the following:

`\cos(55^o)=(s)/(q)`

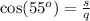
Solving this expression for q, we have:

`\begin{gathered} \cos(55^o)=(s)/(q) \\ q\cos(55^o)=s \\ q=(s)/(\cos(55^o)) \end{gathered}`

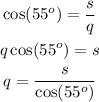
And this is our answer.

`(s)/(\cos(55^o))`