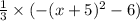Question

Describe the transformation from the graph of f to the graph of h. Write an equation that represents h in terms of x. Look at image for example. Let’s do problem number 11

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given functions.

`\begin{gathered} f(x)=-(x+5)^2-6 \\ h(x)=(1)/(3)f(x) \end{gathered}`

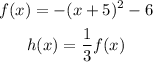
STEP 2: Explain the transformation that occurs

What are Vertical Stretches and Shrinks?

While translations move the x and y intercepts of a base graph, stretches and shrinks effectively pull the base graph outward or compress the base graph inward, changing the overall dimensions of the base graph without altering its shape. When a graph is stretched or shrunk vertically, the x -intercepts act as anchors and do not change under the transformation.

This can be explained further as:

For the base function f (x) and a constant k > 0, the function given by:

Hence, the transformation from the graph is a vertical shrinking by 1/3 factor and the equation that represents h in terms of x is given as:

`(1)/(3)*(-(x+5)^2-6)`