Question

Solve by graphing 6X + 3y equals 12 x + 4y equals 24

Answer 1

The system of equations is:

`\begin{gathered} 6x+3y=12 \\ 8x+4y=24 \end{gathered}`

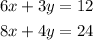
To solve the system of equations by graphing, we need to make a graph of each equation. For that, we solve for y in both equations:

`\begin{gathered} \text{Solving the first equation for y:} \\ 6x+3y=12 \\ 3x=-6x+12 \\ y=-2x+4 \\ \text{Solving the second equation for y:} \\ 8x+4y=24 \\ 4y=-8x+24 \\ y=-2x+6 \end{gathered}`

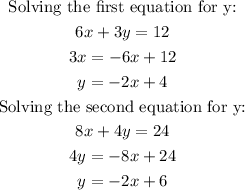
We have two equations to graph:

`\begin{gathered} y=-2x+4 \\ y=-2x+6 \end{gathered}`

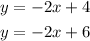
Comparing with the slope-intercept equation:

`y=mx+b`

Where m is the slope and b is the y-intercept.

We can see that the slope of the two equations is m=-2, this means that the lines will have the same rate of change of -2 in y for every 1 in x. And one graph will cross the y-axis at 4 and the other at +6.

The graph of the two equations is shown in the following image:

Where the green line is the first equation, and the red line is the second equation.

There is no solution to this system of equations because the lines do not intersect each other.