Given:
height = 65 m
Given that the object is in free fall, let's solve for the following:
• (a). determine the final speed in m/s.
To find the final velocity, apply the kinematics equation:
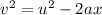
Where:
v is the final velocity
u is the initial velocity = 0
a is the acceleration due to gravity = 9.8 m/s²
x is the displacement = 65 m
Thus, we have:

Therefore the final speed will be -35.69 m/s.
• (c). The distance traveled during the last second of motion before hitting the ground.
To find the distance, apply the formula:
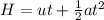
Where:
H is the height.
u is the initial velocity = 0 m/s
t is the time
a is acceleration due to gravity.
Let's rewrite the formula to find the time traveled.
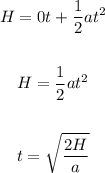
Thus, we have:
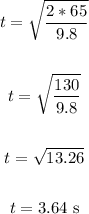
Therefore, the time is 3.64 seconds.
Now, to find the distance traveled during the last second of motion, apply the formula:

Where:
t2 = 3.64 seconds
t1 = 3.64 seconds - 1 second = 2.64 seconds
Thus, we have:
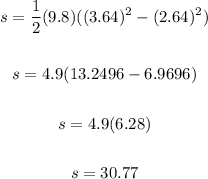
Therefore, the distance in meters, traveled during the last second of motion before hitting the ground is 30.77 meters.
ANSWER:
(A). -35.69 m/s
(C). 30.77 m