Question

Find the equation (in terms of xx ) of the line through the points (-4,1) and (5,-3)

Answer 1

`y=-(4)/(9)x-(7)/(9)`

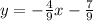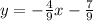
Step-by-step explanation

Given two points of a line, we can find the the equation of that line using the steps below:

• Step 1

Determine the slope of the line, using the formula below:

`\text{slope(m)}=(y_2-y_1)/(x_2-x_1)`

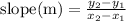
The points given are (-4, 1) and (5, -3). This implies that the coordinates are

x₁= -4 y₁=1 x₂=5 y₂=-3

Substitute the values into the formula and simplify.

`m=(-3-1)/(5+4)=-(4)/(9)`

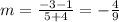
• Step 2

Determine the y-intercept(b) of the line.

Substitute x₁= -4 y₁=1 and m=-4/9 into y=mx + b and solve for intercept(b).

1 = (-4/9)(-4) + b

`1=(16)/(9)+b`

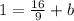
Subtract 16/9 from both-side of the equation.

`b=1-(16)/(9)`

`b=(9-16)/(9)=-(7)/(9)`

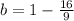
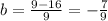
The intercept (b) = -7/9

• Step 3

Form the equation by substituting the value of the slope and intercept into y=mx + b.

Hence, the equation of the line is:

`y=-(4)/(9)x-(7)/(9)`