Question

5. Noah is solving an equation and one of his moves is unacceptable. Hereare the moves he made. Which answer best explains why the "divide eachside by x step is unacceptable? *2(3+6) - 4= 8 + 6321 + 12 - 4= 8 + 612.1 + 8 = 8 + 6.120 = 602 = 6original equationapply the distributive propertycombine like termssubtract 8 from both sidesdivide each side by IO When you divide both sides of 2x = 6x by x you get 2x^2 = 6x^2.When you divide both sides of 2x = 6x by x it could lead us to think that there is nosolution while in fact the solution is x = 0..aWhen you divide both sides of 2x = 6x by x you get 2 = 6x.aOWhen you divide both sides of 2x = 6x by x it could lead us to think that there is nosolution while in fact the solution is x = 3..

Answer 1

Write out the original equation

`2(x+6)-4=8+6x`

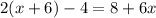
Then, Apply the distributive property on the left hand side of the equation

`\begin{gathered} 2x+12-4=8+6x \\ 2x+8=8+6x \end{gathered}`

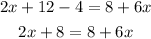
Then combine trhe like terms subtracting 6x from both side

`\begin{gathered} 2x+8-6x=8+6x-6x \\ 2x-6x+8=8 \end{gathered}`

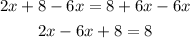
Subtract 8 from both sides of the last equation

`\begin{gathered} 2x-6x+8-8=8-8 \\ 2x-6x=0 \\ -4x=0 \\ \end{gathered}`

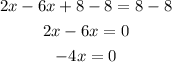
hence

Divide both sides by -4, we have

`\begin{gathered} -(4x)/(-4)=(0)/(-4) \\ \text{Then} \\ x=0 \end{gathered}`

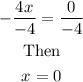
Therefore, the solution is x=0

Hence

When we divide both sides of the equation by x, we have

`\begin{gathered} (2x)/(x)=(6x)/(x) \\ 2=6 \\ \text{which implies thier is no solution} \end{gathered}`

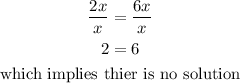
While the solution is x=0

Therefore

When we divide the equation by 2x=6x by x it could lead us to think that there is no solution while the solution is x=0

Answer; The second option is right