ANSWER

Step-by-step explanation
We have that the graph of y is:

It is first reflected about the x axis.
A reflection about the x axis is represented as:
y = -f(x)
which means that we find the negative of the function:
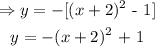
Then, it is translated 3 units up (vertical shift) and 4 units right (horizontal shift).
A translation is represented as:
y = f(x - a) + b
where a = horizontal shift; b = vertical shift
So, we have to find:
y = f(x - 4) + 3
That is:
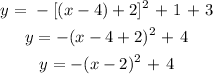
Therefore, that is the equation of the transformed graph.