Question

Writing and evaluating a function modeling continuous exponential growth or decay given two outputs

Answer 1

Step-by-step explanation

The model has the form

`y=ae^(-kt)`

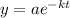
Where a=initial amount

y= final amount

K= growth rate constant

t= time

When 140 kg of substance is left after 7 hours, the formula can be remodeled to be.

`\begin{gathered} 140=400e^(-7k) \\ e^(-7k)=(140)/(400) \\ e^(-7k)=(7)/(20) \\ \ln (e^(-7k))=\ln ((7)/(20)) \\ -7k=\ln ((7)/(20)) \\ k=(\ln((7)/(20)))/(-7) \\ \therefore k=(\ln ((20)/(7)))/(7) \end{gathered}`

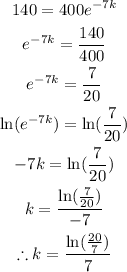
Therefore, the first solution is

`y=400e^{-\ln ((20)/(7))(t)/(7)}`

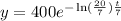
For part b we have 16 hours.

Thus, the answer is 36kg