Given that;
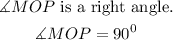
And;
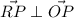
Since line RP is perpendicular to line OP, Angle RPO must be a right angle.
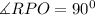
Recall that for two parallel lines intersected by a straight line, Same side interior angles are supplementary.
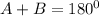
So, for line MO to be parallel to line RP, the sum of angle MOP and angle RPO must be equal to 180 degree.
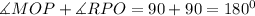
Since the sum of angle MOP and angle RPO is equal to 180 degree, then line MO is parallel to line RP.
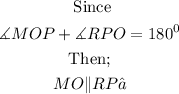
Proved