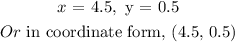Given the equations
x + y = 5----------------------(1)
x - 3y = 3-----------------------(2)
Subtract equation (2) from (1)
x - x -3y - y = 3 - 5
-4y = -2
Divide both -4
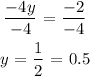
Substitute y = 1/2 into equation (1)
x + y = 5
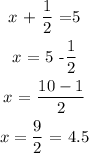
Hence, the solution to the equations is