Question

Pls help! No ive asked 5 tutors and they cant do it!

Answer 1

The sampling distribution can be approximated to follow the normal distribution if the sample size is large, and the values of 'np' and 'n(1-p)' are much greater than 10.

Consider option A,

`\begin{gathered} np=30*0.3=9 \\ n(1-p)=30*(1-0.3)=21 \end{gathered}`

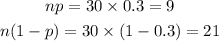
Consider option B,

`\begin{gathered} np=22*0.4=8.8 \\ n(1-p)=22*(1-0.4)=13.2 \end{gathered}`

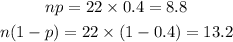
Consider option C,

`\begin{gathered} np=30*0.8=24 \\ n(1-p)=30*(1-0.8)=6 \end{gathered}`

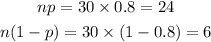
Consider option D,

`\begin{gathered} np=22*0.5=11 \\ n(1-p)=22*(1-0.5)=11 \end{gathered}`

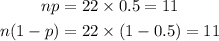
It is observed that only the values in option D, give that 'np' and 'n(1-p)' are greater than 10. Therefore, option D will be the correct choice.