Answer:
Given to solve,
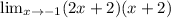
From the rules for limits, we can see that for any polynomial, the limit of the polynomial when x approaches a point k is equal to the value of the polynomial at k.
The given function of the limit is a quadratic function, the limit of the quadratic equation when x approaches a point -1 is equal to the value of the quadratic equation at -1.
we get,
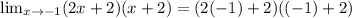
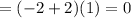
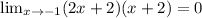
Answer is : 0