The volume V of a cone with radius r and height h is:
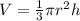
And the radius is half the diameter. Since this cone has a diameter of 12 m, the radius is:
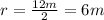
And the height is 8m. Thus, the volume V is:
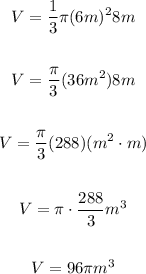
Now, using 3.14 for π, we obtain:
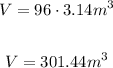
Therefore, the volume of that cone is 301.44m³.