Question

The current in a simple electrical circuit is inversely proportional to the resistance. If thecurrent is 30 amperes (an ampere is a unit for measuring current) when the resistance is 5ohms, find the current when the resistance is 7.8 ohms.

Answer 1

Hello there. To solve this question, we'll have to remember some properties about inversely proportional terms.

Let's start labeling the terms:

Say Current is given by I, Resistance is given by R and voltage is given by V.

By Ohm's Law, we know that:

`V=R\cdot I`

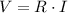
In fact, this is the definition we need to find the answer.

But, to understand why the question mention the fact that they are inversely proportional, note:

We say two numbers x and y are inversely proportional when:

`x\cdot y=k`

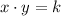
Their product is equal to a constant. k is the constant (of proportionality).

Now, using the given values in the question, we can solve this question.

If the current is 30 ampère when the resistance is 5 ohms, we have to find the current when the resistance is 7.8 ohms.

First scenery:

`V=30\cdot5`

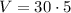
Multiply the numbers

`V=150`

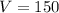
Second scenery:

`V=7.8\cdot I`

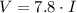
Plugging V = 150, we get:

`150=7.8\cdot I`

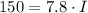
Divide both sides of the equation by a factor of 7.8

`I=(150)/(7.8)`

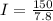
Simplify the fraction by a factor of 2

`I=(75)/(3.9)`

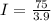
Using a calculator, we get the following approximation

`I\approx19.2\text{ A}`

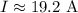
A is for Ampère.