1 Answer

RandomThought · Answer 1 · 2023-12-02T08:17:34+0000

To solve that question we must remember that the sum of all internal angles of a triangle is 180°, we can say that

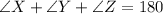
$\angle X+\angle Y+\angle Z=180$

That's a rule! it's always true.

The problem says that

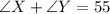
$\angle X+\angle Y=55$

Then let's use it in our equation!

$\begin{gathered} \operatorname{\angle}X+\operatorname{\angle}Y+\operatorname{\angle}Z=180 \\ \\ 55+\operatorname{\angle}Z=180 \end{gathered}$

Now we can solve it for Z

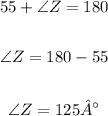
$\begin{gathered} 55+\angle Z=180 \\ \\ \angle Z=180-55 \\ \\ \angle Z=125° \end{gathered}$

Therefore the measure of Z is 125°

Please log in or register to add a comment.