Given
An independent third party found the cost of a basic car repair service for a local magazine.
The mean cost is $217.00 with a standard deviation of $11.40.
To find: The repair costs which would be considered an “unusual” cost.
Step-by-step explanation:
It is given that, the mean is 217.00, and the standard deviation is 11.40.
Consider, the distribution as a Normal distribution.
Then, the first range is defined as,

And, the second range is defined as,
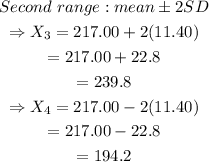
Hence, the answer is option a) 192.53 since it does not belongs to the above ranges.