Given,
The radius of the loop of the roller coaster, r=22.8 m
The forces that are acting on the roller coaster when it is at the top of the loop are the centripetal force directed upwards and the weight of the roller coaster including the passengers directed downwards.
For the passengers to stay in the seat, the centripetal force must be, at the least, equal to the weight of the passengers and the rollercoaster.
That is,
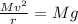
Where M is the combined mass of the rollercoaster and the passengers, v is the minimum speed of the roller coaster when it is at the top of the loop, and g is the acceleration due to gravity.
On simplifying the above equation,
![v=\sqrt[]{gr}](https://img.qammunity.org/2023/formulas/physics/college/mcsiqq4dcfxrsy997p1xer2cqteksmqau7.png)
On substituting the known values,
![\begin{gathered} v=\sqrt[]{9.8*22.8} \\ =14.95\text{ m/s} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/p5lxvgzgutbnk2m5ffyhvylm3tuc2jlowb.png)
Thus the minimum speed that the roller coaster must have when it is at the top of the loop so that the passengers stay in contact with the seats is 14.95 m/s.