Question

A chemical company mixes pure water with their premium antifreeze solution to create an inexpensive antifreeze mixture. The premium antifreeze solution contains 65%pure antifreeze. The company wants to obtain 260 gallons of a mixture that contains 45% pure antifreeze. How many gallons of water and how many gallons of the premium antifreeze solution must be

Answer 1

80 gallons of water

180 gallons of premium antifreeze solution.

Step-by-step explanation:

Let's call X the number of gallons of water and Y the number of gallons of the premium antifreeze solution.

The company wants to obtain 260 gallons of the mixture, so our first equation is:

X + Y = 260

Additionally, the mixture should contain 45% of pure antifreeze and the premium antifreeze solution contains 65% pure antifreeze. So, our second equation is:

0.45(X + Y) = 0.65Y

Now, we need to solve the equations for X and Y. So, we can solve the second equation for X as:

`\begin{gathered} 0.45(X+Y)=0.65Y \\ 0.45X+0.45Y=0.65Y \\ 0.45X=0.65Y-0.45Y \\ 0.45X=0.2Y \\ X=(0.2Y)/(0.45) \\ X=(4)/(9)Y \end{gathered}`

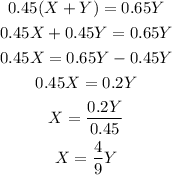
Then, we can replace X by 4/9Y on the first equation and solve for Y as:

`\begin{gathered} (4)/(9)Y+Y=260 \\ (13Y)/(9)=260 \\ 13Y=260\cdot9 \\ 13Y=2340 \\ Y=(2340)/(13) \\ Y=180 \end{gathered}`

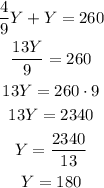
Finally, replacing Y by 180, we get that X is equal to:

`\begin{gathered} X=(4)/(9)Y \\ X=(4)/(9)\cdot180 \\ X=80 \end{gathered}`

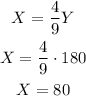
Therefore, the solution should have 80 gallons of water and 180 gallons of premium antifreeze solution.