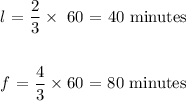The first part of the journey took 4/3 hours (80 minutes)
The last part of the journey too 2/3 hours (40 minutes)
Here, we want to set-up equations to solve
We start by filling the table
Line 1
The rate for the first part of the race is 90 mph
The time for the first part of the race is F
Line 2
The time for the second part of the race is L
The distance (product of the rate and time) is 60L
So, adding these up give us the following equations to be added and solved below;
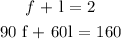
So, we proceed to solve these equations simultaneously
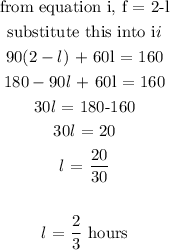
To get f, we simply substitute l into the first part of the equations;
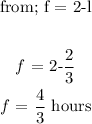
Since an hour is 60 minutes;