Given the parallelogram ABCD
As shown: AB = 4 ft
m∠BAC = 30
m∠BDC = 104
We will find the length of the longer diagonal which will be AC
See the following figure:
The point of intersection of the diagonals = O
The opposite sides are parallel
AB || CD
m∠ABD = m∠BDC because the alternate angles are congruent
So, in the triangle AOB, the sum of the angles = 180
m∠AOB = 180 - (30+104) = 46
We will find the length of OA using the sine rule as follows:
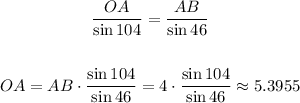
The diagonals bisect each other
So,
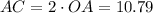
The longer diagonal is AC
Rounding to the nearest tenth
So, the answer will be AC = 10.8 ft