Answer:
The exact perimeter of the square is;
![56\sqrt[]{2}](https://img.qammunity.org/2023/formulas/mathematics/college/dlbzujyocr4isogw666amglbjhopacrlkj.png)
Step-by-step explanation:
Given the square in the attached image.
The length of the diagonal is;
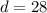
Let l represent the length of the sides;
![\begin{gathered} l^2+l^2=28^2 \\ 2l^2=784 \\ l^2=(784)/(2) \\ l^2=392 \\ l=\sqrt[]{392} \\ l=14\sqrt[]{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/w5iwl7vkzzkcm2cs6y9s28m8yh7jd9l15t.png)
The perimeter of a square can be calculated as;
![\begin{gathered} P=4l \\ P=4(14\sqrt[]{2}) \\ P=56\sqrt[]{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/azx08rwzwv1sjomf2tmmsw4e18ximhgcjb.png)
Therefore, the exact perimeter of the square is;
![56\sqrt[]{2}](https://img.qammunity.org/2023/formulas/mathematics/college/dlbzujyocr4isogw666amglbjhopacrlkj.png)