Question

Line g passes through the points (-2.6,1) and (-1.4.2.5), as shown. Find theequation of the line that passes through (0,-b) and (c,0).

Answer 1

The blue line passes through the points

(-2.6, 1) and (-1.4, 2.5)

I will label the coordinates as follows for reference:

`x_1=-2.6,y_1=1,x_2=-1.4,y_2=2.5`

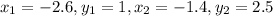
Step 1: Find the slope of the blue line

The slope between two points is calculated with the formula:

`m=(y_2-y_1)/(x_2-x_1)`

We substitute the values and we get that the slope of the blue line is:

`m=(2.5-1)/(-1.4-(-2.6))=(1.5)/(1.2)=1.25`

The slope m of the blue line is 1.25.

step 2: With that slope, calculate b (the intercept of the blue line with the y axis).

For this we use the point - slope equation:

`y=m(x-x_1)+y_1`

Where we will use the sane x1 and x2 as in the previous step, so we get

`\begin{gathered} y=1.25(x-(-2.6))+1 \\ y=1.25(x+2.6)+1 \\ y=1.25x+3.25+1 \\ y=1.25x+4.25 \end{gathered}`

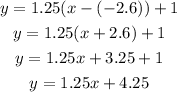
We compare this with the slope-intercept equation

`y=mx+b`

And we can see that the incercept b is 4.25

`b=4.25`

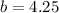
step 3: Find the value of c.

to find the value of c, we need to know at which point the blue line crosses the x axis.

Since we already have the equation of the blue line y=1.25x+4.25, and the line crosses the x axis at y=0, we substitute this to find the x value that is equal to c:

`\begin{gathered} 0=1.25x+4.25 \\ -4.25=1.25x \\ (-4.25)/(1.25)=x \\ -3.4=x \end{gathered}`

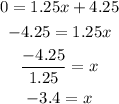
The blue line crosses the x axis at (-3.4,0), thus we can conclude that

`c=-3.4`

Step 4: Define the two point where the orange line passes through.

We know from the picture that the orange line passes through (c,0) and (0,-b)

Since we have the values of c = -3.4 and b=4.25, we can say that the orange line passes through (-3.4, 0) and (0, -4.25)

Step 5: Calculate the slope of the orange line.

the orange line passes through (-3.4, 0) and (0, -4.25), so we define: