Answer:
x = 8
Explanations
From the line geometry shown, the line a and b are parallel lines while line "t" is the transversal.
Since the horizontal lines are parallel, hence;
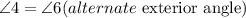
Given the following parameters
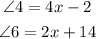
Equate both expressions to have:
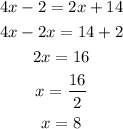
Hence the value of x is 8