Question

Transforming the graph of a function by reflecting over an axis

Answer 1

(a)

(b)

Explanation:

(a)

We must do the following transformation:

`y=f(x)\rightarrow y=f(-x)`

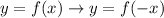
In this case, reflects f(x) about the y-axis. The rule that follows the above, is like this:

`(x,y)\rightarrow(-x,y)`

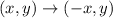
We apply the rule to the points of the function and it would be:

`\begin{gathered} \mleft(-4.2\mright)\rightarrow(4,2) \\ (0,4)\rightarrow(0,4) \\ (4,6)\rightarrow(-4,6) \end{gathered}`

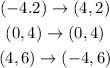
We graph and we have:

(b)

We must do the following transformation:

`y=g(x)\rightarrow y=-g(x)`

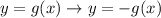
In this case, reflects f(x) about the x-axis. The rule that follows the above, is like this:

`(x,y)\rightarrow(x,-y)`

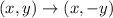
We apply the rule to the points of the function and it would be:

`\begin{gathered} \mleft(-7,-2\mright)\rightarrow\mleft(-7,2\mright) \\ \mleft(-4,-5\mright?)\rightarrow\mleft(-4,5\mright) \\ \mleft(4,-1\mright)\rightarrow\mleft(4,1\mright) \end{gathered}`

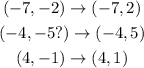
We graph and we have: