Question

Finding the intercepts, asymptotes, domain, and range from the graph of a rational function

Answer 1

From the given graph

The asymptotes are the dotted lines in the graph, then

The vertical asymptote is x = 3

The horizontal asymptote is y = 1

The domain is all values of x that make the function defined

Since x can not equal 3, then

The domain is

`D=(-\infty,3)\cup(3,\infty)`

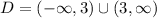
The range is all values of y corresponding to the values of the domain (x)

Since y can not equal 1, then

The range is

`R=(-\infty,1)\cup(1,\infty)`

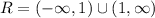
The x-intercept is the value of x at the graph intersecting the x-axis

Since the graph intersects the x-axis at the point (6, 0), then

The x-intercept is 6

The answer is the first choice 6

The y-intercept is the value of y at the graph intersection the y-axis

Since the graph intersects the y-axis at point (0, 2_, then

The y-intercept is 2

The answer is the second answer 2