Question

Question 13 (3 points)

Intel's microprocessors have a 1.8% chance of malfunctioning. Determine the
probability that a random selected microprocessor from Intel will not malfunction.
Write the answer as a decimal.

Answer 1

Step-by-step explanation

The probability that Event A happening is the following:

`P(A)`

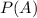
The probability of Event A not happening is the following:

`100-P(A)`

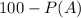
Therefore, we have:

`P(Malfunctioning)+P(Non\text{ Malfunctioning\rparen=100\%}`

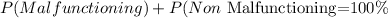
Plugging in the terms into the expression:

1.8 + P(Not malfunctioning) = 100%

Subtracting -1.8 to both sides:

`P(Not\text{ malfunctioning\rparen=100-1.8}`

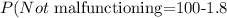
Subtracting numbers:

`P(Not\text{ malfunctioning\rparen=98.2}`

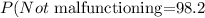
In conclusion, the probability of not malfunctioning is 0.982