The change of base formula states that:
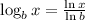
this means that we can caculate any logarithm using the natural logarithm if we make the quotient of the natural logarithm of the original value and the natural logarithm of the original base.
In this case we have:
![\begin{gathered} x=14 \\ b=\sqrt[]{3} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/q5z6vsu3qy1i4kzv9jrou9xblfatx0n2zp.png)
Then, using the change of base formula, we have:
![\log _{\sqrt[]{3}}14=\frac{\ln 14}{\ln \sqrt[]{3}}](https://img.qammunity.org/2023/formulas/mathematics/college/986pvj6evcsvq75u0iz4f2s044tia57gjf.png)
Once we have the expression we just evaluate the expression on the right to get the appoximation we need:
![\log _{\sqrt[]{3}}14=\frac{\ln14}{\ln\sqrt[]{3}}\approx4.804](https://img.qammunity.org/2023/formulas/mathematics/college/ev34j0lzloqtdhmhlwf95g70fcour4fa1h.png)