Effective Rate in Compound Interest
Given r as the nominal rate of investment and n the number of times the interest is compounded annually, the formula for the effective rate is:
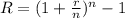
We are required to find the effective rate for a rate of r=4.8% compounded semiannually. This means the value of n is 2 since there are two periods where interest is added to the principal per year.
Substituting the given values in the formula (recall r must be used as a decimal value, i.e. r=4.8/100=0.048):

Calculating:

The effective rate is 4.86%