The given situation can be written in an algebraic way:
Say x the width of the rectangle and y its height.
- The width of a rectangle is 8 inches less than its length:
x = y - 8
- The area of the rectangle is 9 square inches:
xy = 9
In order to find the values of y and x, you first replace the expression
x = y - 8 into the expression xy = 9, just as follow:
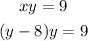
you apply distribution property, and order the equation in such a way that you obtain the general form of a quadratic equation:
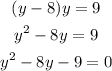
Next, you use the quadratic formula to solve the previous equation for y:
![y=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/gfo69urp8rw17yg122uzk6md9epfe1uf75.png)
here you have a = 1, b = -8 and c = 9. By replacing these values you obtain:
![\begin{gathered} y=\frac{-(-8)\pm\sqrt[]{(-8)^2-4(1)(-9)}}{2(1)}=\frac{8\pm\sqrt[]{64+36}}{2} \\ y=\frac{8\pm\sqrt[]{100}}{2}=(8\pm10)/(2)=(8)/(2)\pm(10)/(2)=4\pm5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/1sdv9q21bs5gev53589zxfv748xxyawnsd.png)
Hence, you have two solutions for y:
y1 = 4 + 5 = 9
y2 = 4 - 5 = -1
You select only the positive solution, because negative lengths do not exist in real life. Hence, you have y = 9.
Finally, you replace the value of y into the expression x = y - 8 to obtain x:
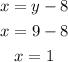
Hence, the width and length of the given recgtangle are:
width = 1 in
length = 9 in