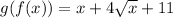Answer:
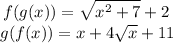
Explanation:
Given the functions f(x) and g(x) below:
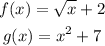
Part A
We want to find the simplified form of f(g(x)).
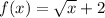
Replace x with g(x):
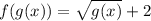
Finally, enter the expression for g(x) and simplify if possible:
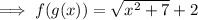
Part B
We want to find the simplified form of g(f(x)). To do this, begin with g(x):
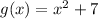
Replace x with f(x):
![g(f(x))=[f(x)]^2+7](https://img.qammunity.org/2023/formulas/mathematics/college/bo6s6tdg8edvt46ob085buuvku1s914j1n.png)
Finally, enter the expression for f(x) and simplify if possible:
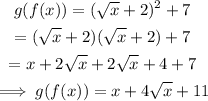
Therefore: