Question

The population of a country dropped from 52.5 million in 1995 to 44.2 million in 2007. Assume that P(t), the population, in millions, t years after 1995, is decreasing according to the exponential decay model.a) Find the value of k, and write the equation.b) Estimate the population of the country in 2018.c) After how many years will the population of the country be million, according to this model?

Answer 1

we have the exponential decay function

`P(t)=52.5(e)^(-0.0143t)`

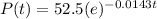
Part b

Estimate the population of the country in 2018

Remember that

t=0 -----> year 1995

so

t=2018-1995=23 years

substitute in the function above

`\begin{gathered} P(t)=52.5(e)^(-0.0143\cdot23) \\ P(t)=37.8\text{ million} \end{gathered}`

Part c

After how many years will the population of the country be 2 ​million, according to this​ model?

For P(t)=2

substitute

`2=52.5(e)^(-0.0143t)`

Solve for t

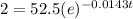
`(2)/(52.5)=(e)^(-0.0143t)`

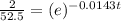
Apply ln on both sides

`\begin{gathered} \ln ((2)/(52.5))=\ln (e)^(-0.0143t) \\ \\ \ln ((2)/(52.5))=(-0.0143t)\ln (e)^{} \end{gathered}`
`\ln ((2)/(52.5))=(-0.0143t)`

t=229 years