To find the square root of a negative number use the next:
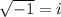
For -6:
You can write -6 as the product of 6 and -1:
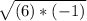
The square root of a product is the same as the product of the square root if each of the factors:
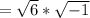
As the square root of 6 is not a exact number (it has many decimals) you leave the square root of 6 as it is. The square root of -1 is i; then, the square root of -6 is:

Then, the square root of -6 is: (√6)i